David A. R. Robin (ENS Paris)
Supervisor: Philippe Rigollet (MIT)

The present document is a word-for-word translation to a web-friendly format of my L3 (Bachelor Sc.) internship report as it was handed on September 2nd, 2018 for review and grading to Pierre Senellart (ENS - INRIA Valda) and Stéphane Mallat (ENS Data). The internship took place from June to August 2018 in Boston, MIT (IDSS). The original report is also available in pdf version. Although not directly credited in the original report, a significant part of the supervision was also carried out by Geoffrey Schiebinger (MIT - Broad Institute). The code produced during this internship was distributed as a python package, and is available on github under broadinstitute/wot [joint work with Joshua Gould (Broad Institute)]. Brevity hereafter is largely due to the hard constraints on length imposed for ENS Internship Reports. This report and the associated presentation were later graded 19 / 20

Contexte

scRNA-Seq

Les récents développements des techniques de séquençage en biologie, et notamment la mise au point du séquençage de cellule unique (Single-cell RNA sequencing en anglais, abbrévié scRNA-Seq), permettent d’observer les processus de développement cellulaire avec une résolution sans précédent. Ces nouvelles données devraient en particulier permettre d’étudier des évolutions qui se déroulent à l’échelle d’une seule cellule, comme la division cellulaire, la réaction à un stimulus extérieur, ou bien la tumorogénèse.

Pour obtenir une telle résolution, il est nécessaire de prélever des cellules du tissu à étudier, puis de les isoler afin d’extraire l’ARN de chacune. On peut alors amplifier cet ARN puis le séquencer pour obtenir le niveau d’expression de chaque gène de la cellule. Mais le processus d’extraction de l’ARN est destructif: la cellule ne survit pas au séquençage. Il est donc impossible d’observer une évolution temporelle avec cette technique, il sera nécessaire de reconstruire ces évolutions à posteriori.

On peut en revanche élever des populations similaires, et effectuer des séquençages à des stades différents du développement. La difficulté devient alors de reconstruire une évolution temporelle détaillée à partir de ces images instantanées de la population de cellules, pour comprendre ce qui s’est passé entre deux images instantanées, notamment quelles cellules de la première ont donné naissance à chaque groupe de la seconde.

Processus stationnaires

Les premières données collectées par scRNA-Seq ciblaient des processus stationnaires: les cellules individuelles évoluent, mais à l’échelle de toute une population, la distribution des cellules semble constante dans le temps. La composante temporelle n’apportait donc aucune information et n’est en conséquence pas présente sur la plupart des données publiées.

C’est pourquoi les algorithmes de reconstruction de trajectoires développés jusqu’à maintenant n’utilisent pas de donnée temporelle, qu’ils remplacent par un concept un peu différent: le pseudotemps. L’idée est de faire correspondre cette valeur de pseudotemps avec le stade d’évolution de la cellule. Deux cellules mesurées au même moment n’ont donc pas nécessairement la même valeur de pseudotemps, mais deux cellules de même avancement dans un processus devraient avoir des valeurs de pseudotemps proches.

Pour reconstruire les trajectoires des cellules d’un processus stationnaire à partir d’une image de la population, on partitionne les données pour isoler des "chemins" disjoints. On peut alors reconstruire la composante temporelle le long de chaque "chemin" en utilisant des données connues sur l’expression de certains gènes à chaque stade de l’évolution.

Processus dynamiques

L’amélioration du séquençage de cellule unique permet aujourd’hui d’observer non seulement des processus stationnaires, mais également des processus dynamiques pour lesquels l’information temporelle est disponible. Il est donc possible d’utiliser cette information pour améliorer la reconstruction des trajectoires là où les méthodes précédemment utilisées échouent:

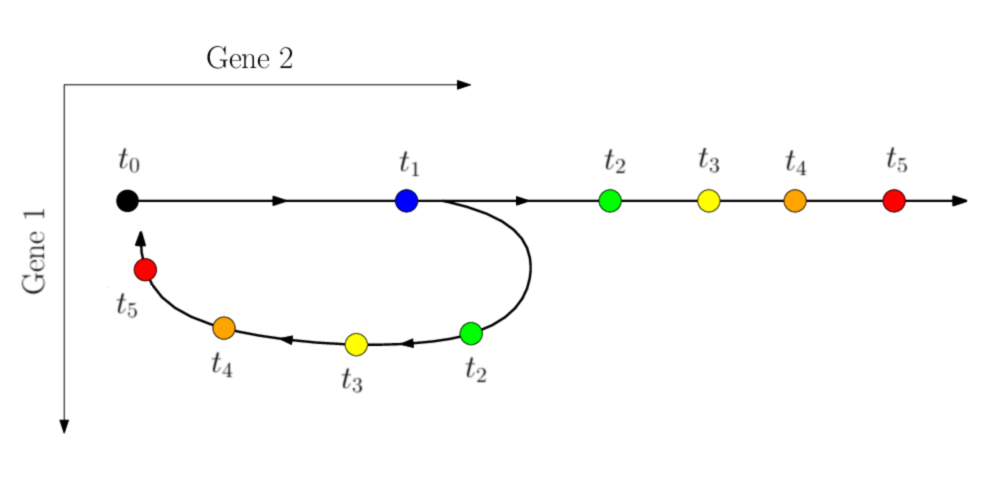
Trajectoire réelle

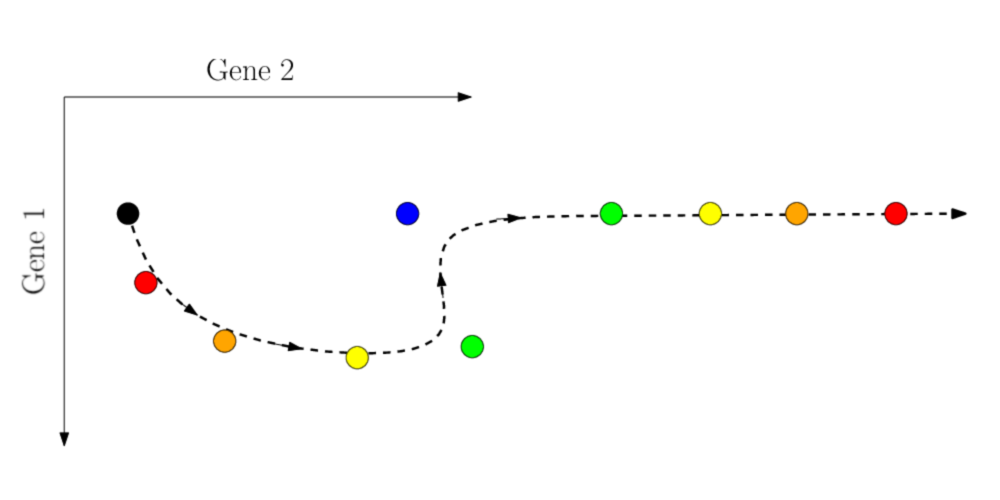
Trajectoire inférée

Figure 1. Processus dynamique nécessitant l'utilisation de l'information temporelle

Le séquençage est destructif, il est donc impossible d’observer une réelle évolution temporelle d’une population de cellules. En revanche, sous l’hypothèse que le nombre de cellules observées est suffisant, on peut considérer que les cellules observées au temps \(t_1\) sont les descendantes des cellules observées au temps \(t_0\) (\(t_0 < t_1\)). Ces cellules ne sont pas à proprement parler des descendantes de la précédente population, mais elles en sont représentatives.

L’opération de reconstruction ne se fera alors plus sur l’ensemble des cellules mesurées, mais uniquement entre les mesures consécutives dans le temps, que l’on se propose de relier au moyen du Transport Optimal.

Cadre théorique

Cellules

Toutes les cellules d’un organisme partagent le même génome, codé dans leur acide désoxyribonucléique (ADN). Ce génome contient en particulier tous les gènes codant des protéines ou des ARN structurés. Tous ces gènes ne sont en revanche pas exprimés de la même façon dans toutes les cellules de l’organisme. Ce sont les niveaux d’expression de ces gènes qui caractérisent la cellule, et sa fonction.

L’ensemble des gènes (noté \(G\)) est fini et fixe pour toute les cellules observées. Le niveau d’expression de chacun de ces gènes peut être représenté par un nombre réel par exemple. On peut alors modéliser une cellule par un vecteur \(x \in \mathbb{R}^G\) dans l’espace d’expression génétique. Dans cet espace, chaque dimension correspond à un gène, et la coordonnée \(x_i\) d’un vecteur représentant une cellule indique le niveau d’expression du gène \(i\) dans ladite cellule. On utilisera abusivement le terme "cellule" pour un désigner un vecteur \(x \in \mathbb{R}^G\) modélisant une cellule.

La trajectoire spatiale d’une cellule porte peu d’information du point de vue biologique. Nous choisirons donc de ne pas la prendre en considération. Toutes les occurences des mots "trajectoire" ou "position" qui suivent se réfèrent à l’espace d’expression génétique défini ci-dessus.

Populations

On définit une configuration d’une population de cellules comme une mesure sur l’espace d’expression génétique. Par exemple, on peut représenter l’ensemble des cellules \(\{\, x_i \mid i < n \,\}\) par

\[\mathbb{P}_t = \sum_{i < n} \delta_{x_i}\]

où \(\delta_{x_i}\) désigne une mesure de Dirac au point \(x_i\).

Cette mesure de Dirac vient du fait que la cellule a été mesurée à une position unique bien précise, mais on peut se représenter la probabilité de présence de la cellule comme ayant un support plus large.

Les configurations mesurables par scRNA-Seq sont toujours de cette forme car seul un nombre fini de cellules peut être mesuré. En revanche, pourvu que le nombre de cellules observées soit suffisament grand, on peut considérer que ces configurations empiriques à support fini sont représentatives de la configuration "réelle" des cellules, que l’on se représente intuitivement comme étant plutôt continue.

Un processus de développement est alors une fonction qui à un temps associe une configuration. On notera \(T\) l’ensemble des temps considérés, et les processus de développement \(\mathbb{P}_t\) pour \(t \in T\).

Couplages

Un couplage de deux distributions \(\mathbb{P}\) et \(\mathbb{Q}\) sur \(\mathbb{R}^G\) est une distribution \(\pi\) sur \(\mathbb{R}^G \times \mathbb{R}^G\) qui admet \(\mathbb{P}\) et \(\mathbb{Q}\) comme lois marginales, i.e.

\[\forall A \subset \mathbb{R}^G,\quad \int_{x \in A} \int_{y \in \mathbb{R}^G} \pi(x, y) \cdot dx dy = \mathbb{P}(A)\] \[\forall B \subset \mathbb{R}^G,\quad \int_{y \in B} \int_{x \in \mathbb{R}^G} \pi(x, y) \cdot dx dy = \mathbb{Q}(B)\]

On étendra cette définition à des mesures sur \(\mathbb{R}^G\) sans imposer de contrainte sur leur somme. \(\pi\) sera alors également une mesure, satisfaisant toujours les contraintes ci-dessus. On utilisera de plus les notations suivantes:

\[\forall A \subset \mathbb{R}^G,\, B \subset \mathbb{R}^G, \quad \pi(A, B) = \int_{x \in A} \int_{y \in B} \pi(x, y) \cdot dx dy\] \[\forall A \subset \mathbb{R}^G,\quad \pi(A, \mathord{\cdot}) = (\, y \,\mapsto\, \int_{x \in A} \pi(x, y) \cdot dx \, )\]

Opérateurs

Intuitivement, on peut comprendre \(\pi\) comme une carte indiquant comment déplacer une masse initialement dans la configuration \(\mathbb{P}\) vers la configuration \(\mathbb{Q}\). Le coefficient \(\pi(x, y)\) indique dans ce cas combien de masse doit partir du point \(x\) pour aller au point \(y\).

On peut alors définir l’opérateur \(\pi_\#\), qui à une mesure associe l’image de cette mesure par la carte \(\pi\).

\[\pi_\# : \mu \, \mapsto \, \pi(\mathbb{R}^G,\, \cdot) = \int_{x \in \mathbb{R}^G} \pi(x, \mathord{\cdot}) \cdot d\mu(x)\]

On peut de la même façon définir l’opérateur qui transporte dans l’autre sens:

\[\pi^\# : \nu \, \mapsto \, \pi(\cdot,\, \mathbb{R}^G) = \int_{y \in \mathbb{R}^G} \pi(\mathord{\cdot}, y) \cdot d\nu(x)\]

Si \(\pi\) est un couplage entre \(\mathbb{P}\) et \(\mathbb{Q}\), alors on a

\[\pi_\# \mathbb{P} = \mathbb{Q} \quad \quad \text{et} \quad \quad \pi^\# \mathbb{Q} = \mathbb{P}\]

L’hypothèse du transport optimal

La position des cellules est mesurée aux temps \(t_0\) et \(t_1\) par scRNA-Seq. On souhaite à partir de ces mesures obtenir des informations héréditaires sur les cellules, c’est à dire savoir quelles cellules au temps \(t_1\) descendent d’un ensemble de cellules données du temps \(t_0\) par exemple. Les mesures ne portent pas à priori suffisamment d’information pour pouvoir reconstituer les trajectoires des cellules entre les temps \(t_0\) et \(t_1\). En revanche, on peut formuler une hypothèse supplémentaire qui permet de le faire:

Hypothèse: Le transport des cellules entre deux configurations observées est optimal

Cette hypothèse stipule qu’une population de cellules, pour passer d’une configuration à une autre, suit une trajectoire qui minimise le coût global de cette transformation, où le coût est défini par la modification de l’expression des gènes de chaque cellule, i.e. la distance séaprant les les cellules dans l’espace d’expression génétique.

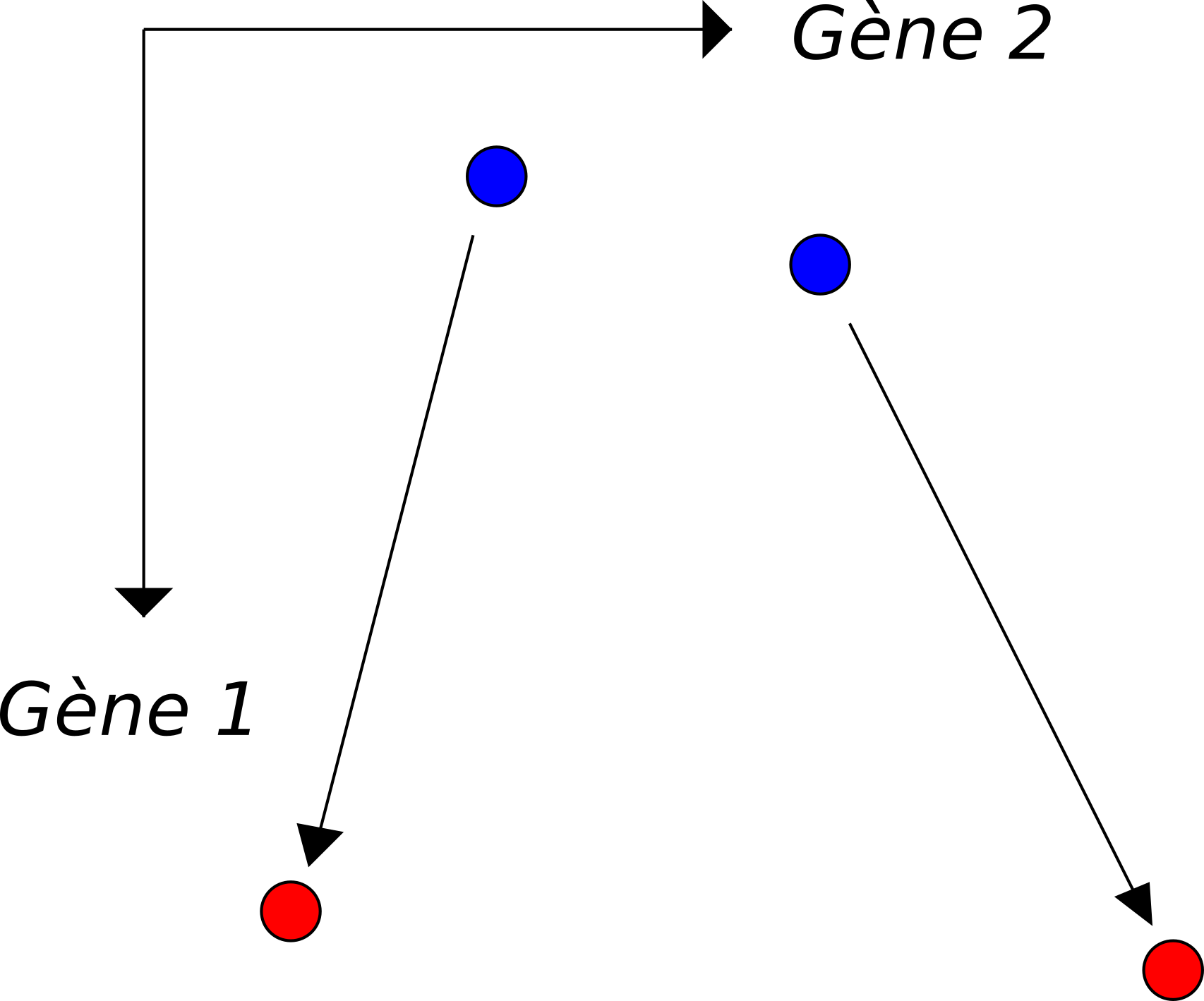
Faible modification

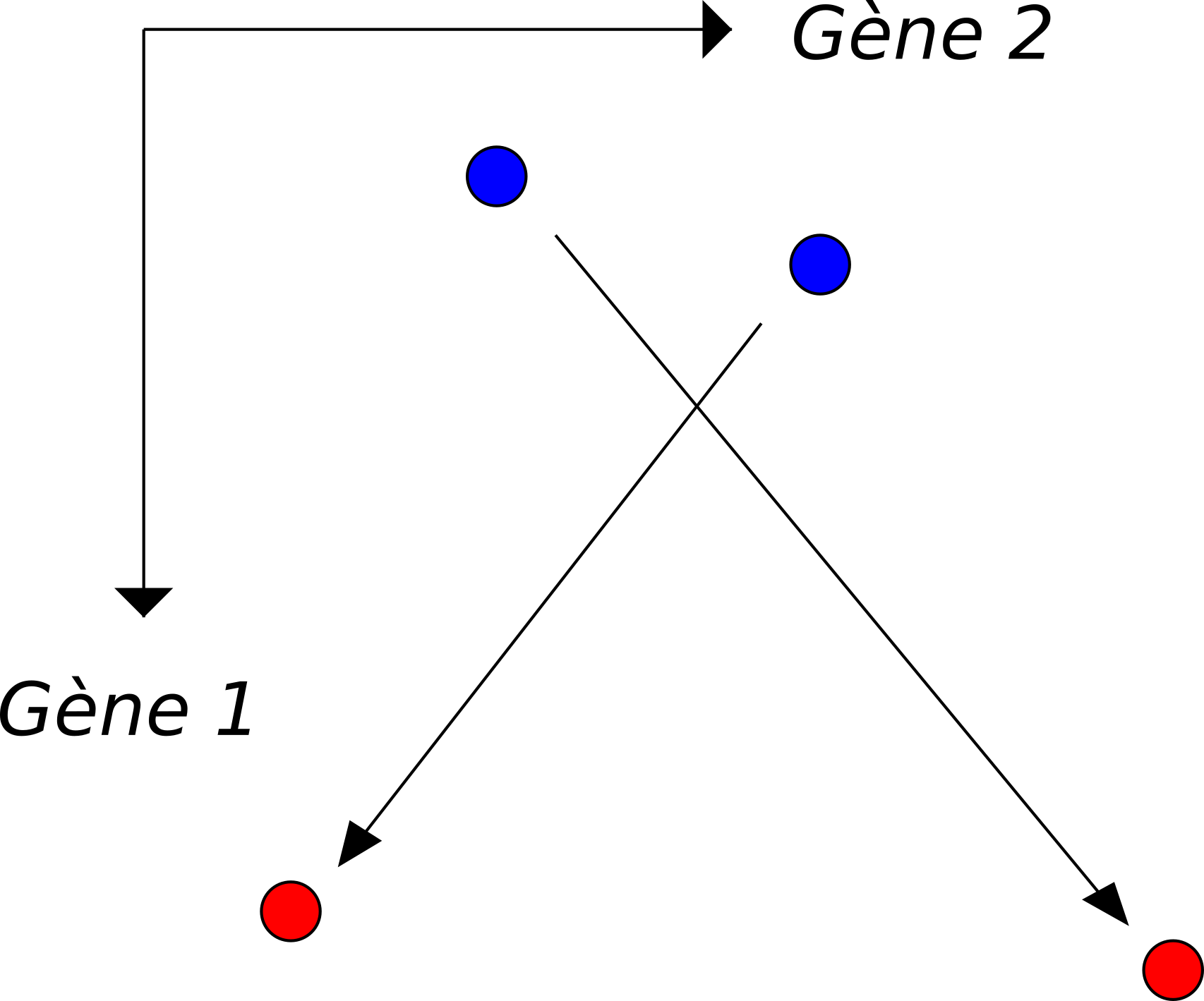
Forte modification

Figure 2. Deux transports avec différentes modifications de l'expression du gène 2

Pour obtenir des cellules dans la second configuration, il est moins "coûteux" de modifier légèrement l’expression de quelques gènes (ici le gène 2) sur une cellule déjà proche dans l’espace d’expression génétique, plutôt que de devoir modifier beaucoup l’expression d’un nombre conséquent de gènes sur une cellule initialement plus éloignée.

Sur une échelle de temps suffisamment courte, l’expression génétique des cellules change relativement peu, il devrait donc être possible d’inférer les trajectoires des cellules à partir des images instantanées.

Transport Optimal

Présentation

Une des images les plus simples associées au transport optimal est celle du transport de sable. Une certaine quantité de sable se trouve initialement dans une configuration \(\mathbb{P}\), et doit être déplacée vers une autre configuration \(\mathbb{Q}\). Le transport d’une masse \(m\) de \(A\) à \(B\) est associé à un coût \(m \cdot c(A, B)\), linéaire en \(m\) et variant suivant la distance qui sépare \(A\) et \(B\) par exemple. Le problème est alors de trouver une façon de déplacer le sable de la première configuration vers la seconde en minimisant la somme des coûts des transports effectués.

La façon de transporter le sable entre ces deux configurations est caractérisée par une carte de transport, un couplage entre \(\mathbb{P}\) et \(\mathbb{Q}\), qui au couple \((A, B)\) associe la masse qui doit être transportée de \(A\) à \(B\).

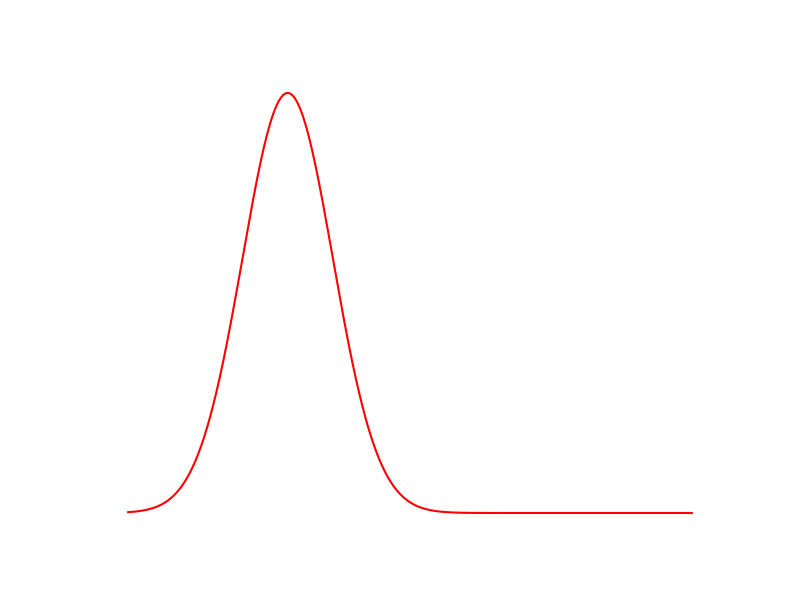
Distribution source

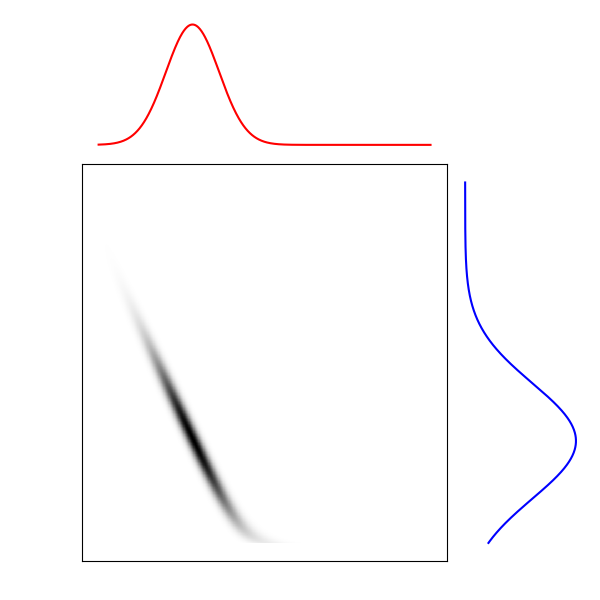
Carte de transport

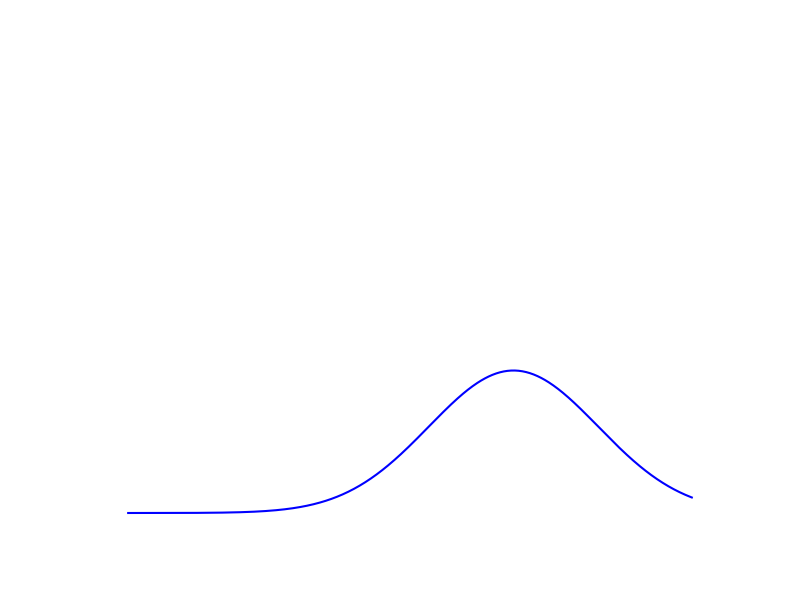
Distribution cible

Figure 3. Carte de transport entre deux distributions

Cette carte de transport permet d’associer les points de la distribution initiale et les points vers lesquels ils seront transportés dans la distribution cible. Il est alors possible de reconstruire la trajectoire du tas de sable en admettant que la vitesse de chaque grain de sable est constante. C’est cette application qui nous intéresse ici, car les distributions interpolées sont plus représentatives des populations de cellules qu’une simple moyenne pondérée des deux distributions par exemple. Elles ont de plus l’avantage de donner pour chaque grain de sable une trajectoire continue de la première distribution à la seconde.

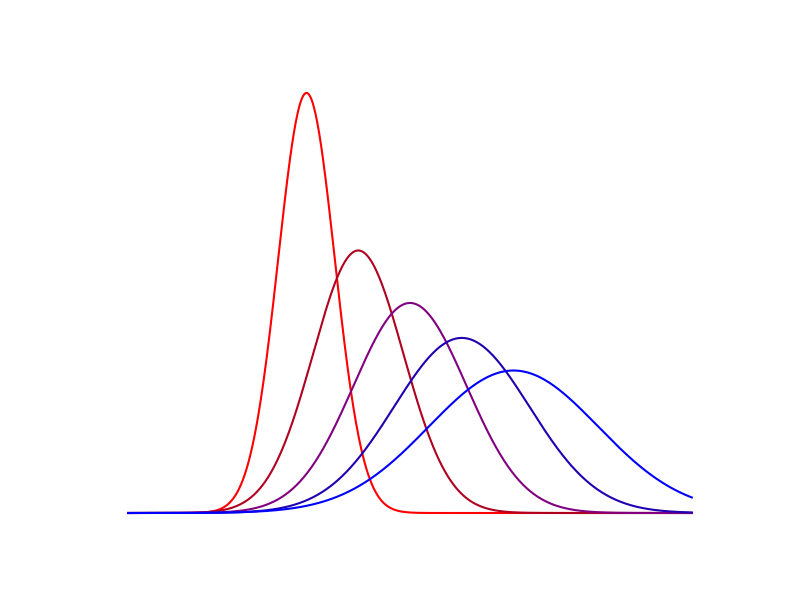
Avec la carte de transport

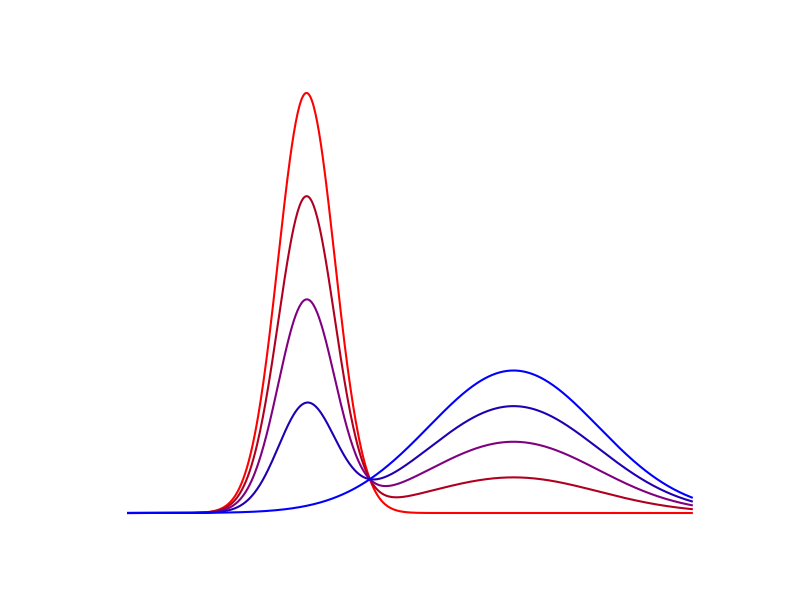
Par moyenne pondérée

Figure 4. Interpolation entre les deux distributions considérées

Le problème du transport optimal a de nombreuses autres applications, notamment dans le traitement d’images, car il fournit une distance intrinsèque entre deux images (le coût de transport). Ceci permet de classifier efficacement des images, mais également de supprimer des éléments de premier plan, de transférer les couleurs d’une image sur une autre, ou bien de reconstituer des séquences vidéos tronquées par interpolation. On retrouve donc ce problème dans l’imagerie médicale, l’astronomie, ou bien la météorologie.

Image originale

Couleurs à transférer

Résultat

Figure 5. Transfert de couleurs entre deux images

Pour transférer des couleurs d’une image à une autre, il suffit de considérer chaque pixel comme un point de l’espace tridimensionnel des couleurs, puis de transporter le nuage de points correspondant à une figure vers celui correspondant aux couleurs de l’autre. La carte de transport ainsi obtenue associe à chaque couleur de la première image une couleur de la seconde, en minimisant la somme des distances entre les couleurs initiales et modifiées de chaque pixel. Il suffit alors d’altérer la première image pour refléter ces nouvelles couleurs.

Formalisation

Si \(c(x, y)\) représente le coût du transport d’une unité de masse du point \(x\) au point \(y\), alors le coût total du transport d’une population par la carte \(\pi\) est donné par:

\[\int_x \int_y c(x, y) \cdot \pi(x, y) \cdot dx dy\]

On cherche alors à trouver la carte de transport optimale, c’est à dire le couplage de \(\mathbb{P}\) et \(\mathbb{Q}\) qui minimise ce coût.

Dans le cas où les deux distributions marginales ont un support fini, la carte de transport optimale a également un support fini, qui est le produit des supports marginaux. Elle peut alors être représentée par une matrice, de même que la fonction de coût, puisqu’il n’est plus nécessaire d’en connaître les valeurs en dehors dudit support.

Le coût associé à une carte de transport \(\pi\) s’écrit alors:

\[\langle \, c \, , \, \pi \, \rangle = \sum_x \sum_y c(x, y) \cdot \pi(x, y)\]

Le problème du transport optimal peut donc se réécrire de la façon suivante:

\[\min_{\pi \in \Gamma (\mathbb{P}, \mathbb{Q})} \, \langle \, c \, , \, \pi \, \rangle\] \[\text{où} \quad \Gamma (\mathbb{P}\,,\, \mathbb{Q}) = \{ \,\pi \,:\, \pi \cdot 1 = \mathbb{P}\, , \, \pi^T \cdot 1 = \mathbb{Q} \,\}\]

Afin de conserver la forme générale du problème, on continuera d’utiliser une fonction de coût quelconque dans la suite, mais on peut avoir à l’esprit un cas simple, qui sera celui utilisé dans un premier temps pour la reconstruction de trajectoires: le carré de la distance euclidienne.

\[c(x, y) = {\lVert x - y \rVert}^2\]

Régularisation

Des algorithmes très rapides ont été développés pour résoudre ce problème dans le cas où on ajoute une pénalisation entropique (\(\mathcal{H}(\pi) = - \mathbb{E}_\pi (\log \pi)\)), car celle-ci rend le problème fortement convexe.

La carte de transport optimal correspond alors au problème modifié:

\[\min_{\pi \in \Gamma (\mathbb{P}, \mathbb{Q})} \, \langle\, c \,,\, \pi \,\rangle - \varepsilon \mathcal{H}(\pi)\]

Plus le paramètre de régularisation \(\varepsilon\) est élevé, et plus l’entropie de la carte a d’importance dans la fonction d’objectif. Ceci se caractérise souvent par un support de la carte optimale plus étendu, comme on peut le constater sur la figure ci-dessous.

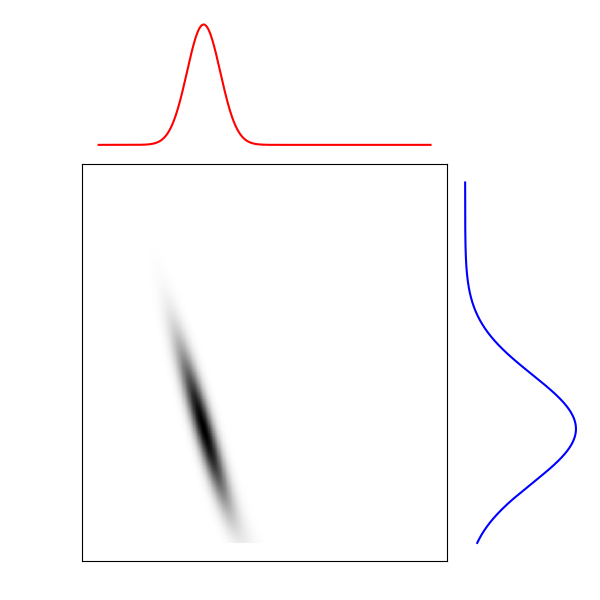
$$\varepsilon = 10 ^ 3$$

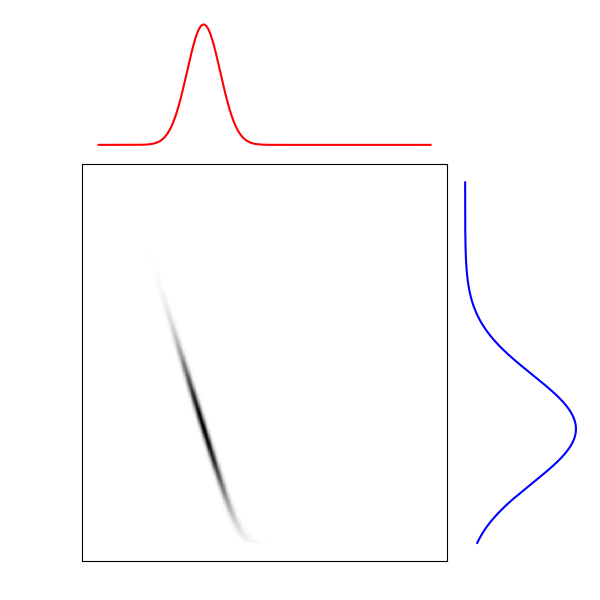
$$\varepsilon = 10 ^ 2$$

Figure 6. Cartes de transport optimal pour différentes valeurs de $$\varepsilon$$

Transport Optimal et croissance cellulaire

Croissance cellulaire

L’image du transport de sable a l’avantage de donner facilement une première intuition en ce qui concerne le transport optimal. Mais les cellules ont une particularité que le sable n’a pas: elles peuvent se multiplier, ou mourir. Pour pouvoir prendre en compte ce phénomène, il est nécessaire de pouvoir estimer le taux de croissance des cellules. On peut ajouter une hypothèse permettant de le faire plus facilement:

Hypothèse: la position \(x\) d’une cellule détermine son taux de croissance \(g(x)\).

Cette hypothèse est acceptable car beaucoup de gènes entrent en considération dans la division cellulaire et l’apoptose (mort programmée d’une cellule). En connaissant les niveaux d’expression de tous ces gènes, on peut raisonnablement penser qu’il est possible de déterminer la probabilité que la cellule se divise ou meurt, d’où la connaissance du taux de croissance moyen.

Si on note \(r(x, y)\) la masse qui est transportée de \(x\) vers \(y\), alors la masse qui arrive en \(y\) après croissance, est \(r(x,y) \cdot {g(x)}^{\Delta t}\)

On choisira donc pour les contraintes marginales du problème non plus \(\mathbb{P}\) et \(\mathbb{Q}\), mais \(\mathbb{P} \odot g ^ {\Delta t}\) et \(\overline{g} \cdot \mathbb{Q}\),

Le facteur \(\overline{g} = \sum_i \mathbb{P}_i \, {g_i}^{\Delta t}\) est nécessaire car pour que le transport soit possible, il faut que les deux marginales soient de même mesure.

Transport optimal non équilibré

La position de la cellule, même mesurée avec un peu de bruit, nous permet d’estimer son taux de croissance. Il ne s’agit en revanche que d’une estimation, et il convient d’élargir un peu le modèle précédent pour accepter une petite incertitude sur ce taux. On peut par exemple assouplir les contraintes marginales en n’imposant pas une égalité stricte, mais en pénalisant la différence par rapport aux marginales attendues:

\[\min_{\pi} \quad \langle\, c \,, \pi \,\rangle - \varepsilon \mathcal{H}(\pi) + \lambda_1 \cdot \text{KL}(\pi \cdot 1 \,||\, \mathbb{P} \odot g^{\Delta t}) + \lambda_2 \cdot \text{KL}(\pi^T \cdot 1 \,||\, \overline{g} \, \mathbb{Q})\]

où \(\text{KL}\) est la divergence de Kullback-Leibler:

\[\text{KL} (P \, ||\, Q) = \sum_x P(x) \cdot \log \frac{P(x)}{Q(x)}\]

Apprentissage de la croissance cellulaire

La pénalisation ajoutée permet d’obtenir:

\[\sum_y \pi(\mathord{\cdot},\, y) \approx \overline{g} \, \mathbb{Q}\] \[\sum_x \pi(x,\, \mathord{\cdot}) \approx \mathbb{P} \odot g ^ {\Delta t}\]

La somme sur une ligne de \(\pi\) peut donc être légèrement différente de celle imposée par notre taux de croissance estimé, si cela diminue suffisament le coût total du transport: une nouvelle valeur du taux de croissance est "apprise" par l’algorithme.

On peut alors essayer de relancer l’algorithme avec cette fois \(g = \pi \cdot 1\), pour tenter d’affiner encore le résultat en utilisant comme contrainte marginale non plus le taux de croissance estimé, mais le taux de croissance appris.

Résolution algorithmique

L’algorithme de Sinkhorn

Il est possible de réécrire la fonction d’objectif du transport équilibré comme une projection:

\[\min_{\pi \in \Gamma (\mathbb{P}, \mathbb{Q})} \, \langle\, c \,,\, \pi \,\rangle - \varepsilon \mathcal{H}(\pi) = \min_{\pi \in \Gamma (\mathbb{P}, \mathbb{Q})} \, \varepsilon \,\text{KL}(\pi \, || \, K)\] \[\text{avec} \quad K = \exp( - c / \varepsilon)\]

La carte de transport optimale peut être vue comme la projection de \(K\) sur \(\Gamma (\mathbb{P}, \mathbb{Q})\). On peut alors utiliser les projections alternées de Bregman pour la calculer. On pose pour cela les deux espaces affines

\[\mathcal{C}_1 = \{\, \pi \,:\, \pi \cdot 1 = \mathbb{P} \,\} \quad \quad \text{et} \quad \quad \mathcal{C}_2 = \{\, \pi \,:\, \pi^T \cdot 1 = \mathbb{Q} \,\}\]

et on projete itérativement sur chacun, i.e. on normalise alternativement les colonnes puis les lignes de \(\pi\) pour que la contrainte marginale considérée soit satisfaite, jusqu’à obtenir \(\pi \in \mathcal{C}_1 \cap \mathcal{C}_2\). Les projections s’écrivent

\[\mathcal{P}_{\mathcal{C}_1} (\pi) = \text{diag}\left(\frac{\mathbb{P}}{\pi \cdot 1}\right) \cdot \pi \quad \quad \text{et} \quad \quad \mathcal{P}_{\mathcal{C}_2} (\pi) = \pi \cdot \text{diag}\left(\frac{\mathbb{Q}}{\pi^T \cdot 1}\right)\]

On multiplie pour chaque projection à gauche ou à droite par une matrice diagonale. On a donc que pour tout \(n\), \(\pi^{(n)}\) est de la forme \(\text{diag}(a^{(n)}) \cdot \pi^{(0)} \cdot \text{diag}(b^{(n)})\). L’algorithme de Sinkhorn consiste à mettre à jour successivement \(a\) et \(b\), jusqu’à atteindre la condition d’arrêt souhaitée:

\[\pi^{(n)} = \text{diag}(a^{(n)}) \cdot K \cdot \text{diag}(b^{(n)})\] \[a^{(n)} = \frac{\mathbb{P}}{K \cdot b^{(n)}} \quad \quad \text{et} \quad \quad b^{(n+1)} = \frac{\mathbb{Q}}{K^T \cdot a^{(n)}}\]

Ces itérations ont l’avantage de ne faire intervenir que des produits matrice-vecteur, qui seront très rapide et parallélisable sur machine.

Extension au transport non-équilibré

Il est possible de généraliser ces itérations à toutes fonctions de pénalisation des marginales \(F_1\) et \(F_2\). On avait jusqu’ici utilisé

\[F_1(z) = \iota_{\{=\}}(z,\, \mathbb{P}) \quad \quad \text{et} \quad \quad F_2(z) = \iota_{\{=\}}(z,\, \mathbb{Q})\] \[\text{avec} \quad \iota_{\{=\}}(x, y) = \begin{cases} 0 &\quad \text{si} \quad x = y\\ + \infty &\quad \text{sinon} \end{cases}\]

Pour utiliser une pénalisation différente, il suffit de modifier les itérations:

\[a^{(n)} = \frac{\text{prox}_{F_1 / \varepsilon}(K \cdot b^{(n)})}{K \cdot b^{(n)}} \quad \quad \text{et} \quad \quad b^{(n+1)} = \frac{\text{prox}_{F_2 / \varepsilon}(K^T \cdot a^{(n)})}{K^T \cdot a^{(n)}}\] \[\text{avec} \quad \text{prox}_{F / \varepsilon}(z) = \underset{s}{\operatorname{argmin}} \,F(s) + \varepsilon\,\text{KL}(s \,||\, z)\]

On peut alors appliquer ce résultat à la pénalisation assouplie des marginales décrite plus haut,

\[F_1 = \lambda_1 \, \text{KL}(\,\cdot\,||\,\mathbb{P}) \quad \quad \text{et} \quad \quad F_2 = \lambda_2 \, \text{KL}(\,\cdot\,||\,\mathbb{Q}) \quad \quad \text{donnent}\] \[a^{(n)} = {\left(\frac{\mathbb{P}}{K \cdot b^{(n)}}\right)}^{\frac{\lambda_1}{\lambda_1 + \varepsilon}} \quad \quad \text{et} \quad \quad b^{(n+1)} = {\left(\frac{\mathbb{Q}}{K^T \cdot a^{(n)}}\right)}^{\frac{\lambda_2}{\lambda_2 + \varepsilon}}\]

Cet algorithme est suffisant pour résoudre le problème du transport optimal régularisé non équilibré, mais nous allons tout de même utiliser lors de son implémentation quelques techniques qui permettront d’une part de limiter les erreurs numériques dûes à la représentation en machine des flottants, et d’autre part de diminuer un peu le temps de calcul nécessaire pour obtenir une solution satisfaisante avec des valeurs extrêmes pour \(\varepsilon\), \(\lambda_1\) ou \(\lambda_2\).

Modification du coût

On utilise pour les projections la variable \(K = \exp ( - c / \varepsilon)\).

Certains coefficients de \(K\) sont alors arrondis à \(0\) si les valeurs de \(c\) correspondantes sont trop élevées, ce qui rend ces valeurs indifférentiables dans la suite de l’algorithme. On peut limiter ce problème en normalisant \(c\). En effet, la carte de transport optimale est invariante par application d’un facteur multiplicatif à \(c\). On choisira donc de conserver toujours pour \(c\) une médiane de \(1\).

Le calcul de la matrice de coût doit être effectué pour chaque paire de populations pour lesquelles on veut calculer une carte de transport. Son calcul s’effectue cependant en \(\mathcal{O}(n^2G)\) où \(n\) est la taille des populations considérées. Ce facteur \(G\) est en pratique assez fortement limitant car le nombre de gènes mesurés est généralement de l’ordre de \(20\,000\).

Pour limiter le coût de calcul de cette matrice, on choisit d’utiliser l’analyse en composantes principales pour projeter linéairement les cellules dans un espace de petite dimension (de l’ordre de quelques dizaines). Cette projection permet de limiter l’influence des dimensions contenant majoritairement du bruit, pour ne conserver que les dimensions intéressantes. En effet, une large majorité des gènes n’est exprimé dans aucune des cellules mesurées pendant l’expérience, si bien que la dimension qui lui correspond dans l’espace d’expression génétique ne contient que du bruit.

Stabilisation logarithmique

Dans le cas où \(\varepsilon\) prend des valeurs très faibles, les coefficients des variables \(a\) et \(b\) peuvent devenir trop grands pour être représentés en machine. Il devient alors nécessaire d’appliquer une étape de stabilisation pour éviter les erreurs numériques. Un moyen efficace de prévenir ces erreurs est de stocker non pas la variable \(a\), mais plutôt deux variables, la variable duale \(u\) et la variation par rapport à celle-ci, \(\tilde{a}\). L’idée est de garder la variable stabilisée \(\tilde{a}\) proche de 1, et d’absorber le reste sous forme logarithmique à travers la variable \(u\), car on a

\[a = \tilde{a} \cdot \exp\left(u / \varepsilon\right) \quad \quad \text{et} \quad \quad b = \tilde{b} \cdot \exp\left(v / \varepsilon\right)\]

Il convient alors de modifier les itérations précédemment définies pour utiliser les variables stabilisées.

On utilise pour cela le noyau stabilisé \(\tilde{K}\):

\[\tilde{K}_{i, j} = \exp(\,(\, u_i + v_j - c_{i, j}\,)\,/\, \varepsilon\,)\]

et les itérations deviennent:

\[\tilde{a}^{(n)} = {\left(\frac{\mathbb{P}}{K \cdot \tilde{b}^{(n)}}\right)}^{\frac{\lambda_1}{\lambda_1 + \varepsilon}} \odot \exp(-\frac{u}{\lambda_1 + \varepsilon})\] \[\tilde{b}^{(n+1)} = {\left(\frac{\mathbb{Q}}{K^T \cdot \tilde{a}^{(n)}}\right)}^{\frac{\lambda_2}{\lambda_2 + \varepsilon}} \odot \exp(-\frac{v}{\lambda_2 + \varepsilon})\]

Ce qui nous donne l’algorithme complet:

Algorithm under migration to HTML, please come back later or check the pdf version

Départ à chaud

Cet algorithme converge beaucoup plus rapidement lorsque la valeur de \(\varepsilon\) est élevée. De plus, les cartes de transport optimales pour deux valeurs de \(\varepsilon\) différentes sont relativement proches. Pour accélérer le calcul des cartes avec une valeur très faible pour \(\varepsilon\), on peut donc effectuer un départ "à chaud". On commence par calculer \(u\) et \(v\) pour une valeur de \(\varepsilon\) plus élevée, ce qui est rapide, puis on diminue progressivement \(\varepsilon\) et on recalcule la carte de transport, en utilisant à chaque fois pour l’initialisation de \(u\) et \(v\) les valeurs précédemment obtenues. Comme les valeurs de \(u\) et \(v\) sont déjà très proches de l’optimum, la convergence est obtenue rapidement à chaque étape.

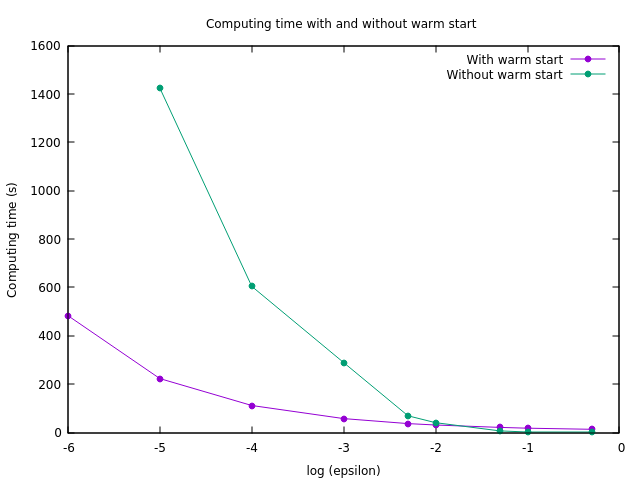
Figure 7. Performances de l'algorithme avec et sans le départ à chaud

Critère d’arrêt

On souhaite garantir que lorsque l’algorithme s’arrête, le résultat retourné est raisonnablement proche de l’optimum recherché. Pour cela, on utilisera la version duale du problème. Si \(x\) représente une solution possible du problème (une carte de transport), et \(f\) la fonction d’objectif utilisée, alors le problème s’écrit sous la forme:

\[\min_x \,f(x)\]

On peut reformuler le problème sous sa forme duale:

\[\max_x \,g(x^{*})\]

où \(x^{*}\) est une solution duale associée à la solution primale \(x\), et \(g\) la fonction d’objectif duale associée à \(f\). On a alors

\[\forall x,\quad f(x) \geq g(x^{*})\] \[\text{et} \quad x \,\,\text{est optimale} \Rightarrow f(x) = g(x^{*})\]

Si \(\pi\) est la solution optimale du problème primal, on a toujours

\[f(x) - f(\pi) \leq f(x) - g(x^{*})\]

On choisira donc comme critère d’arrêt \(f(x) - g(x^{*}) \leq \tau\) pour un certain \(\tau\).

L’évaluation de ce critère d’arrêt s’effectue en \(\mathcal{O}(n^2)\), avec \(n\) la taille des configurations considérées. En effet, le calcul de \(f\) et \(g\) nécessite l’utilisation de la matrice \(K\), qui est de taille \(n^2\). En pratique, l’évaluation du critère d’arrêt après chaque itération constitue près de 99 \% du temps de calcul pour \(n = 1000\).

Afin de limiter un peu ce coût, on peut changer le critère d’arrêt pour les premières phases du départ à chaud, et n’utiliser le critère plus coûteux que lorsque \(\varepsilon\) a atteint sa valeur finale. On peut pour les premières phases attendre que la variation des variables \(\tilde{a}\) et \(\tilde{b}\) tombent sous un certain seuil, car cette évaluation s’effectue en \(\mathcal{O}(n)\) et que la garantie d’optimalité lors de ces premières phases n’est pas nécessaire, il s’agit seulement d’initialiser \(u\) et \(v\) pour accélérer la phase finale.

Validation de l’hypothèse

Idée générale

L’hypothèse initiale était que le transport des cellules entre deux configurations mesurées est optimal, et cette hypothèse devait nous permettre de reconstruire les trajectoires cellulaires entre ces deux configurations. On peut désormais tester cette hypothèse et vérifier que l’on est effectivement capable de retrouver des configurations intermédiaires de façon fiable.

Pour cela, on procède de façon localisée: on choisit trois mesures consécutives, aux temps \(t_0\), \(t_{0.5}\) et \(t_1\). Les cellules aux temps \(t_0\) et \(t_1\) (populations que l’on nommera \(P_0\) et \(P_1\)) joueront le rôle des deux mesures consécutives entre lesquelles on veut reconstruire la trajectoire des cellules, et les cellules au temps \(t_{0.5}\) (population \(P_{0.5}\)) serviront à contrôler la qualité du résultat. On peut alors construire la carte de transport de \(t_0\) à \(t_1\), puis interpoler au temps \(t_{0.5}\) une population reconstruite estimée \(I_{0.5}\), et calculer la distance entre \(I_{0.5}\) et \(P_{0.5}\).

La distance que nous utiliserons pour cela est une distance entre mesures sur \(\mathbb{R}^G\), dite "distance du cantonnier" (Earth Mover’s Distance), ou "métrique de Wasserstein". Il s’agit du coût de transport entre ces deux mesures, dans le cas non-régularisé et équilibré, i.e. \(d (P, Q) = \min_{\pi \in \Gamma (P,\,Q)} \,\langle\, c \,,\, \pi \,\rangle\)

Pour améliorer un peu cette mesure de qualité, on peut partitionner les données de chaque mesure en groupes de tailles comparables (\(P_t^{(i)}\) pour chaque \(i\)). On interpole alors une population \(I_{0.5}^{(i, j)}\) entre \(P_0^{(i)}\) et \(P_1^{(j)}\) pour toute paire \((i,\,j)\), et on peut la comparer aux \(P_{0.5}^{(k)}\). On obtient donc un ensemble de distances \({(\, d(I_{0.5}^{(i,j)},\, P_{0.5}^{(k)})\,)}_{i, j, k}\), que l’on peut comparer aux distances entres les groupes réels \({(\, d(P_{0.5}^{(k)},\, P_{0.5}^{(l)})\,)}_{k \neq l}\).

Si l’interpolation est efficace, ces distances devraient être proches, c’est à dire que la distance entre un groupe interpolé et un groupe réel est sensiblement égale à la distance entre deux groupes réels, auquel cas on concluera que ce processus a reconstruit des groupes plausibles le long de la trajectoire suivie par les cellules.

Interpolation

Pour interpoler une population entre deux populations \(P\) et \(Q\), on commence par calculer une carte de transport \(\pi\) les reliant. Le coefficient \(\pi_{i, j}\) correspond alors à la masse allant de \(P_i\) à \(Q_j\). On rappelle que ce coefficient prend en compte la croissance cellulaire, c’est à dire que l’on peut le décomposer en \(\pi_{i, j} = r_{i, j} \cdot g_{i}^{\Delta t}\), où \(r_{i, j}\) est la masse partant de \(P_i\) pour aller en \(Q_j\) sans croissance, \(g_i\) le taux de croissance de cette masse pendant ce trajet, et \(\Delta t\) la durée du trajet. On supposera que ce taux de croissance est constant pendant le trajet car les mesures sont suffisamment rapprochées pour que les cellules ne se déplacent pas trop entre deux mesures.

Lorsque l’on souhaite interpoler à une fraction \(\alpha \in [0, 1]\) de ce trajet, toute la croissance n’a pas encore eu lieu. Il faudra donc utiliser \(\tilde{\pi}\), défini par \(\tilde{\pi}_{i,j} = r_{i, j} \cdot g_i^{\alpha \cdot \Delta t}\), où \(g\) est le taux de croissance qui a été appris, i.e. \(g = \pi \cdot 1\).

La population interpolée est alors la mesure \(\mu\) de support \(\{\,I_{i,j}\,\}\) telle que:

\[\mu \,:\, I_{i,j} \mapsto \tilde{\pi}_{i, j} = r_{i,j} \cdot g_i^{\alpha \cdot \Delta t}\] \[\text{avec} \quad I_{i, j} = (1 - \alpha) \cdot P_i + \alpha \cdot Q_j\]

Simulations

Lors des essais qui ont conduit au choix de l’algorithme et des techniques de stabilisation décrites plus haut, ainsi que lors des tests destinés à vérifier le bon fonctionnement de la validation, il était nécessaire de ne pas utiliser le seul jeu de données réelles auquel nous avions accès, afin de ne pas adapter l’outil à ce jeu de données précis plutôt qu’à l’ensemble des cas de figure dans lequel il peut être utilisé.

Une simulation relativement simple mais complète est celle du bruit gaussien autour d’un ensemble de chemins. Pour générer des données dans ce cadre de simulation, on commence par se donner un ensemble de chemins. Chaque chemin est une fonction continue de \([0, 1]\) dans \(\mathbb{R}^G\) représentant la trajectoire d’un certain type de cellule. Pour chaque temps \(t\) auquel on souhaite générer des données, on attribue un poids à chaque chemin, et on génère une cellule autant de fois que nécessaire, de la façon suivante: on tire au hasard un chemin \(\phi\) (suivant les poids choisis plus haut), et on choisit la cellule \(\phi(t) + X_\phi\), où \(X_\phi\) suit une loi normale de dimension \(\mid G \mid\) dépendant éventuellement du chemin choisi \(\phi\).

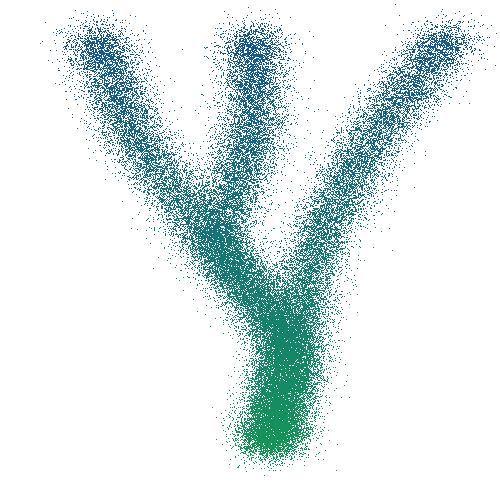
Figure 8. Exemple de donées simulées en deux dimensions avec trois chemins

Ce cadre de simulation a permis d’effectuer des premiers tests très prometteurs concernant l’utilisation du transport optimal. Les résultats de l’un d’entre eux sont présentés dans la figure ci-dessous. On y voit les trois chemins qui évoluent en parallèle dans le quart haut gauche (\(P_0\) est en rouge, \(P_{0.5}\) en violet, et \(P_1\) en bleu). On observe dans la moitié basse de la figure la reconstruction par interpolation, qui donne un résultat nettement meilleur que la reconstruction randomisée. Le quart haut droit présente l’évolution temporelle (sous forme de leur moyenne et variance) des différentes distances permettant de comparer les résultats des deux reconstructions.

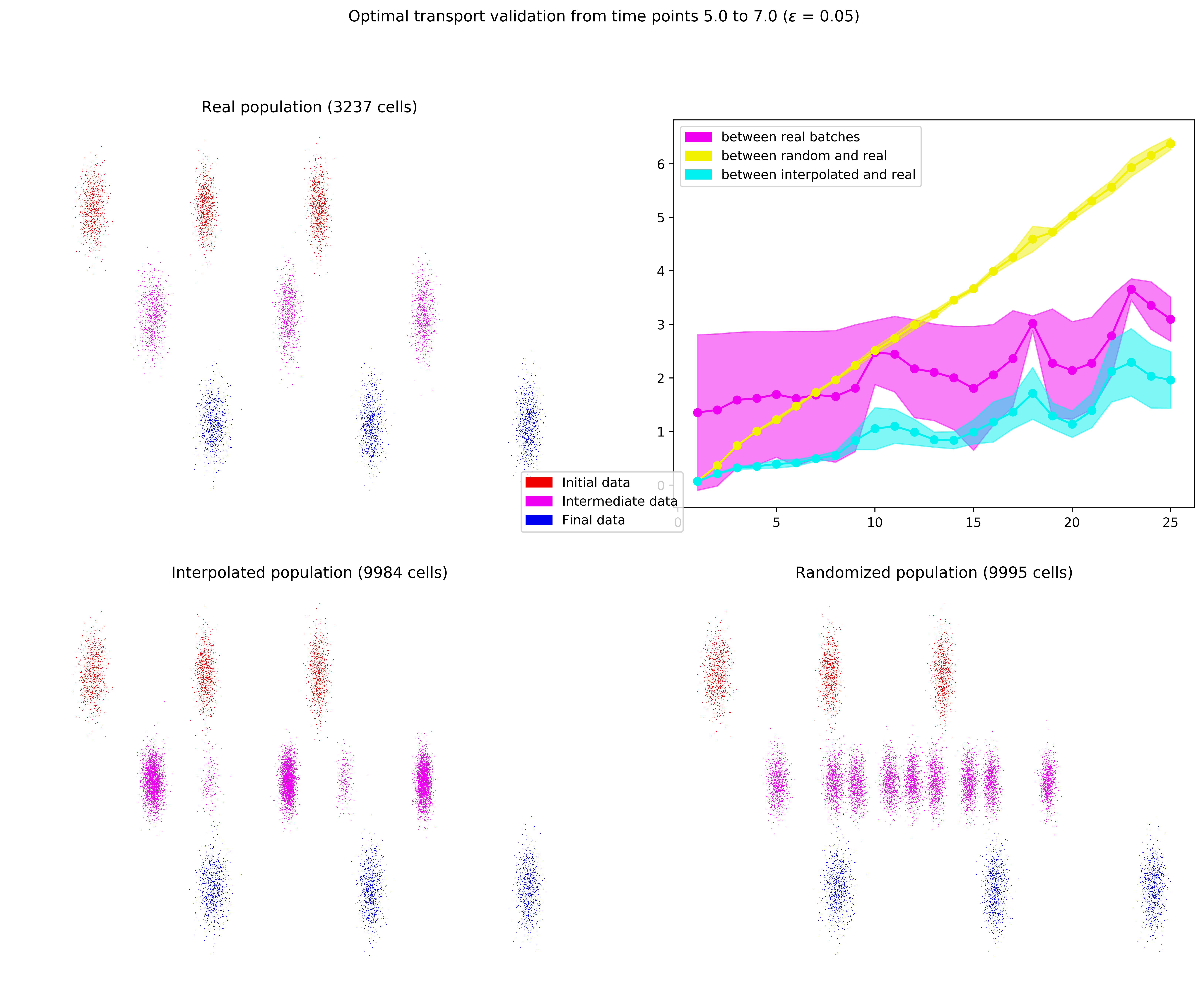
Figure 9. Résultats de la reconstruction par transport optimal par rapport à ceux de la reconstruction randomisée sur des données simulées par bruit gaussien autour de trois chemins évoluant en parallèle

Autres hypothèses

Pour vérifier que la population \(I_{0.5}\) interpolée par transport optimal est une bonne approximation de la population réelle \(P_{0.5}\), on propose de considérer également d’autres approximations, afin de pouvoir comparer leurs performances.

On représentera l’utilisation de la première ou de la dernière configuration comme configuration reconstruite. Cela revient à dire que \(P_0\), ou bien \(P_1\), sont de bonnes approximations de \(P_{0.5}\).

Une autre approximation que l’on représentera est celle qui consiste à reconstruire une population entre \(P_0\) et \(P_1\) de façon randomisée: on pioche au hasard un élément \(p_0 \in P_0\) et \(p_1 \in P_1\), ce qui nous donne un point intermédiaire \((1 - \alpha) \cdot p_0 + \alpha \cdot p_1\). On répète ensuite cette opération jusqu’à obtenir le nombre de points souhaités.

Résultats

On peut alors essayer toutes ces reconstructions sur des données réelles pour évaluer les résultats du Transport Optimal en comparaison. Les données réelles sur lesquelles nous avons effectué ces évaluations sont des fibroblastes d’embryons de souris, qui sont reprogrammés en cellules souches pluripotentes induites par une injection de sérum au jour 8. Un total de 40 mesures ont été effectuées.

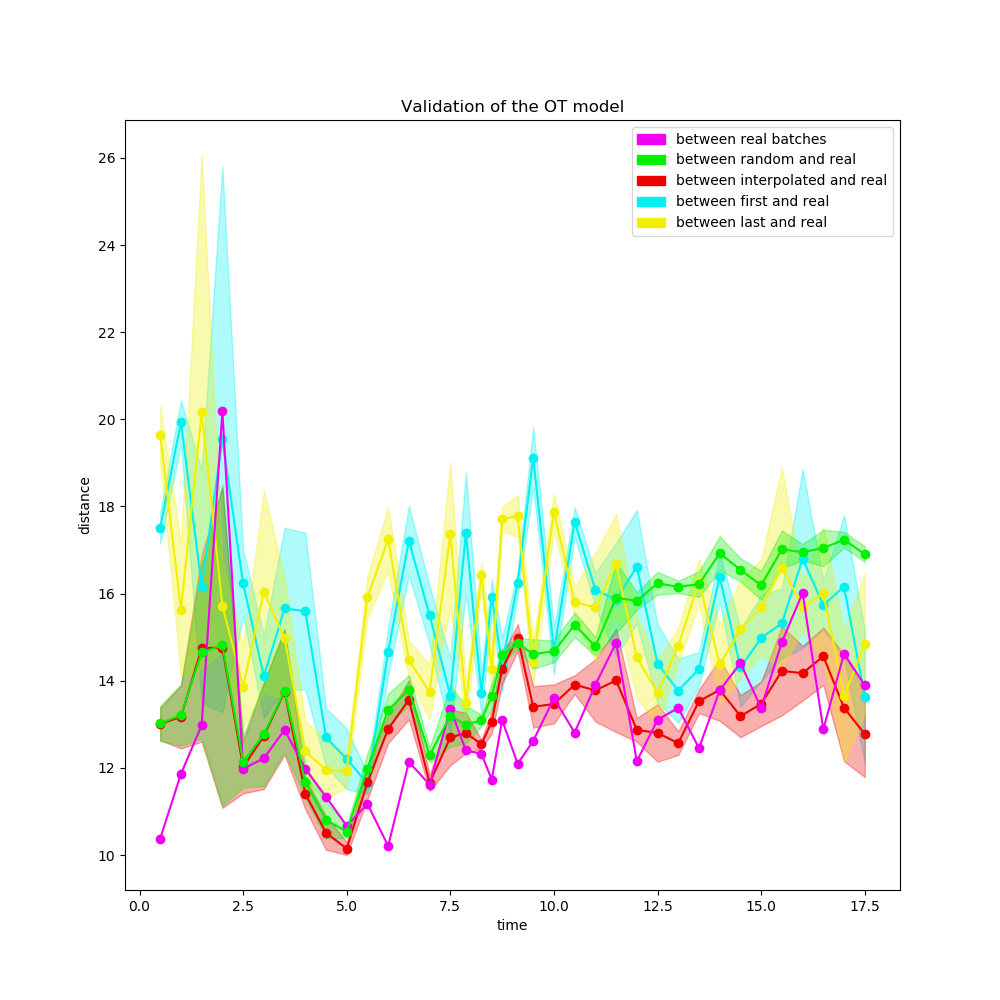
Figure 10. Résultats des différentes méthodes d'approximation sur des données réelles

Dans un premier temps, les cellules sont toutes très proches les unes des autres, si bien que la reconstruction randomisée et la reconstruction par Transport Optimal sont très proche. À mesure que les cellules se divisent en groupes différents, les résultats de la reconstruction par Transport Optimal deviennent sensiblement meilleurs que ceux des autres méthodes.

Visualisation en deux dimensions

Une des difficultés rencontrées à la fois lors des tests et des présentations des résultats est l’absence de représentation graphique des configurations de cellules. En effet, celles-ci sont situées dans un espace de \(20\,000\) dimensions qu’il est difficile de se représenter autrement que sous la forme d’une matrice. Cependant, un changement de point de vue sur les données permet de visualiser les populations en deux dimensions: on peut voir l’ensemble des cellules non pas comme des points d’un espace de haute dimension, mais comme les noeuds d’un graphe complet, où le poids d’une arrète est la distance reliant ses deux extrémités. Il est alors possible d’utiliser des algorithmes de visualisation de graphes pour voir une vue d’ensemble de toutes les cellules.

Les résultats de "Force-directed layout embedding" par exemple ont la particularité de bien isoler les trajectoires sur les données réelles auxquelles nous avions accès. La couleur (du violet au jaune) sur la figure ci-dessous correspond au temps auxquels les cellules ont été mesurées. On retrouve les trois chemins qui ont servi à la génération des données, confondus au départ, puis bien isolés par la suite.

Figure 11. Résultats de force-directed layout embedding sur les données simulées ci-dessus

Conclusion

Les résultats de la validation sur données réelles permettent de conclure que l’objectif initial de reconstruction des trajectoires entre deux mesures est assez largement atteint. Les réseaux de régulation des gènes qui peuvent être échafaudés grâce aux trajectoires reconstruites ont déjà permis de retrouver de nombreux résultats biologiques connus, et même de nouveaux résultats sur la reprogrammation des fibroblastes, qui restent cependant à confirmer.

L’algorithme établi plus haut, ainsi que tous les scripts de validation et de prétraitement des données, ont été mis en ligne sous la forme d’un paquet Python: wot (pour Waddington Optimal Transport), développé en partenariat avec le Broad Institute de Boston, qui a fourni les données réelles utilisées pour la validation (non encore publiées). Ce paquet fait usage de l’algorithme sus-cité pour construire les cartes de transport, et calcule les ancêtres ou descendants de configurations de cellules grâce à ces cartes, en utilisant un cache sur le disque dur pour éviter de recalculer des cartes de transport inutilement et en parallélisant autant que possible le calcul de ces dernières.

Les résultats obtenus ici ne sont en revanche qu’une toute petite étape sur le chemin de la reconstruction des trajectoires cellulaires réelles. En effet, nous n’avons considéré que des mesures à support fini, alors qu’il serait souhaitable de travailler avec des distributions de probabilité continues, dont les mesures seraient issues, plutôt que de considérer les mesures comme des points de passage obligés. Il ne s’agit en quelque sorte que de reconstructions affines par morceaux là où la fonction que l’on cherche à reconstruire est beaucoup plus régulière.

Au delà de la réalisation de ce projet, ce stage a été également pour moi l’occasion de faire mes premiers pas dans le monde de la recherche au sein d’une équipe extrêment sympathique et passionnée par son travail. J’ai pu progresser sur un plan technique, et théorique puisqu’il s’agissait également de mes premiers pas dans l’optimisation convexe, mais aussi apprendre beaucoup sur le plan de la communication, à la fois parce que l’équipe travaillait en anglais et parce qu’elle était composée de mathématiciens et de biologistes, qui n’ont pas les mêmes modèles à l’esprit, et des pédagogies différentes dans leur façon de présenter des résultats ou des hypothèses.

Références